素数可以说是数论中最基础,也是最重要的概念,指的是一个大于2的正整数,除了1和它本身之外,不是任何数的倍数。2013年5月,新罕布什尔大学的数学家张益唐发表了一篇关于素数研究的标志性论文,第一次提出了有无穷对素数,之间存在着一定的间隔。他还证明了这个间隔是在7000万以内。论文发表之后,短短时间内就有许多数学家掌握了他的新方法,开始尝试改进这个常数。从7000万到6000万,再到4200万、1300万、500万、40万,到目前为止,这个常数已经降到了246,越来越接近孪生素数猜想的范围。如果这一常数改进到2,就相当于证明了孪生素数猜想。

1985年,保罗·爱多士(左)正与陶哲轩在讨论数学。2014年8月,陶哲轩和另外四位数学家证明了爱多士的猜想,成为76年来有关素数间隔问题的最重大突破。

素数间隔问题

加州大学洛杉矶分校的陶哲轩说,这是他有能力解决的第一个爱多士的有奖问题。

牛津大学的詹姆斯·梅纳德写了两篇新论文中的第二篇,证明了爱多士关于大素数间隔的猜想。
到此为止,数学家们在反过来的一个问题——连续素数的间隔可以有多远?——上已经取得了76年来第一个重要进展。随着数字增长,相邻素数之间的平均间隔会趋于无穷,但在任一有限的数字列中,最大的素数间隔可以比平均间隔大很多。没有人能计算出这些间隔到底有多大。
“这是一个很显而易见的问题。在谈论到素数的时候,这是首先要问的问题之一,”蒙特利尔大学的数论学家安德鲁·格兰维尔(Andrew Granville)说,“但对问题答案的探索停滞了几乎80年时间。”
2014年8月,两个数学研究小组发表了文章,论述了如何证明保罗·爱多士关于素数间隔的猜想。两个团队已经联合起来,进一步深化素数间隔问题的研究结果,并预计于12月再发表一篇新的论文。
保罗·爱多士(Paul Erd?s)是20世纪成果最为丰硕的数学家之一,终其一生解决了数百个数学问题,并热衷于为数学问题的解决提供现金奖励。尽管大部分的奖励只有25美金,但爱多士“有点儿鲁莽地”(他自己后来写道)提供了一份1万美金的奖励,用于解决他提出的素数间隔猜想的证明问题。
爱多士的猜想基于苏格兰数学家罗伯特·亚历山大·兰金(Robert Alexander Rankin)在1938年提出的一个看似奇怪的边界。兰金称,对于足够大的数X,小于X的最大素数间隔至少为:
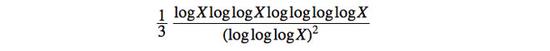
加州大学洛杉矶分校的陶哲轩说,在数论公式中会出现许多的“log”(自然对数的简写)。他与伊利诺伊大学香槟分校的凯文·福特(Kevin Ford)、牛津大学的本·格林(Ben Green)以及莫斯科斯捷洛夫数学研究所的谢尔盖(Sergei Konyagin)合作撰写了两篇新论文中的一篇。
不过,兰金的结果是“一个不可理喻的公式,你永远不可能自然地展示出来,”陶哲轩说,“所有人都认为这个公式很快就会得到改进,因为它太奇怪了。”然而,在超过七十年的时间里,依然没有人能对兰金的公式进行哪怕最微不足道的改进。
许多数学家认为,最大素数间隔很可能大得多——大于(log X)2的数量级。这一理论是由瑞典数学家哈拉尔德·克拉梅尔(Harald Cramér)在1936年首先提出来的。(log X)2数量级的素数间隔是在素数表现得像随机数的集合——在很多方面它们看起来的确如此——时会出现的。但是,没有人能接近证明克拉梅尔的猜想。陶哲轩说:“我们对素数的了解还不是很多。”
爱多士提出了一个更为温和的猜想:可以随意用一个大的数字取代兰金公式中的1/3,只要你在数字列表上取的数字足够大。这意味着素数间隔可以比兰金公式所呈现的大很多,但仍小于克拉梅尔的猜想。
新的两种证明爱多士猜想的方法都基于一个建立大素数间隔的简单方法。一个大的素数间隔相当于两个素数之间的一长列非素数(或称复合数)。这里介绍一个建立100个复合数列表的简单方法。先从数字2,3,4,…,101,开始,然后每个数加上101的阶乘(101!)。这列数字就变成101! + 2, 101! + 3, 101! + 4, … , 101! + 101。因为101!可以被从2到101的数字整除,因此这列数字的每个数都是复合数,即101! + 2可以被2整除,101! + 3可以被3整除,以此类推。“所有关于大的素数间隔的证明采用的方法,都只是这一高中代数方法的细微变形。”牛津大学的詹姆斯·梅纳德(James Maynard)说道。他撰写了两篇新论文中的第二篇。
上面所列的复合数是非常大的,因为101!具有160位。为了改进兰金的公式,数学家们需要建立更小一点的复合数列表——在类似2,3,4,…,101这样的列表上加上一个更小的数字,获得复合数列表是可能的。两个团队对有关素数间隔的最新研究结果(各自不同)进行了分析。梅纳德的论文采用了他自己去年开发的工具,研究了素数之间的较小间隔。
现在,上述的五位研究者已经联合起来,重新设定新的边界,并计划在一周或两周内发布一篇预印稿。陶哲轩认为,这篇论文利用现有的方法,将兰金的基础方法尽可能地进行了延伸。
这项新工作并不能立即投入应用,但了解大的素数间隔将最终影响加密算法的研究。梅纳德称,如果存在比克拉梅尔猜想所预测的更长的复合数列表,那将会给依赖于寻找大素数的加密算法带来麻烦。“如果他们很不走运,在一个巨大间隔的开端开始寻找,那这个算法就会耗费很长的运行时间。”
对于素数间隔,陶哲轩有着更加个人化的研究动机。“一段时间之后,你会感到这些东西在嘲笑你,”他说,“你被认为是研究素数的专家,但你回答不了这些基础的问题,即使人们已经对此思考了好几个世纪。”
保罗·爱多士于1996年逝世,但另一位与他广泛合作的数学家,来自加州大学圣地亚哥分校的罗纳德·格雷厄姆(Ronald Graham)决定好好处理这1万美金的奖项。
1985年,10岁的神童陶哲轩在一次数学活动中遇到了爱多士。“他平等地对待我,”这位2006年赢得数学界最高荣誉菲尔兹奖的数学家回忆道,“和我谈论了非常严肃的数学问题。”现在,陶哲轩已经第一次有能力解决爱多士提供奖励的问题。“所以这其实挺酷的,”他说道。
格兰维尔说,近期有关素数间隔的研究进展已经催生出新一代的数论学家,他们认为一切都是可能的。“在我学习数学的成长时期,我们以为这些问题将是永恒的,不会看到有人能够回答,直到另一个时代的到来,”他说,“但我觉得,过去一两年中,人们的态度已经改变。有许多年轻人比过去的人更有野心,因为他们已经看到了实现重大突破的可能。”

